• 數學解題程式設計教學

格子路徑

• 講義

• 尤拉計畫網站 第15題

  從 \(2 \times 2\) 方格的左上角出發，沿著向右或向下的路徑前進，最後到達右下角，總共有 6 種不同的走法。

  

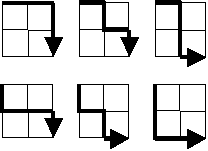
  【最後目標】

  從 \(20 \times 20\) 方格的左上角出發，沿著向右或向下的路徑前進，最後到達右下角，總共幾種不同的走法？

  ---

  假設在一個 \(5 \times 3\) 的方格紙中

  

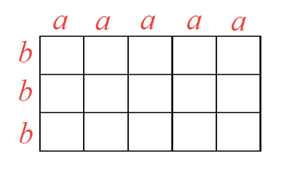
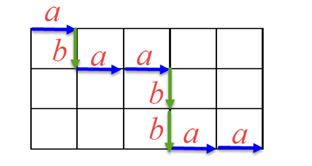
  每一橫列小段稱為 a，每一縱列小段稱為 b，從左上到右下的每一條相異路徑，必然通過 5 個 a，且通過 3 個 b，這 8 個字母的排列順序，對應到為一個路徑，如下圖的路徑對應為 abaabbaa

  

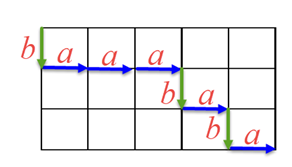
  又如下圖的路徑對應為baaababa

  

  請問 5 個 a、3 個 b 的排列方法有多少呢？

  5+3=8，總共有8個元素要排列，因此可排列出 \(8! = 8 \times 7 \times 6 \times 5 \times 4 \times 3 \times 2 \times 1\) 種不同排法。

  因為 5 個 a 沒有順序性，因此重覆出現了 \(5! = 5 \times 4 \times 3 \times 2 \times 1\) 次。

  因為 3 個 b 沒有順序性，因此重覆出現了 \(3! = 3 \times 2 \times 1\) 次。

  所以總共有 \(\frac{(5+3)!}{5! 3!}\) 種不同的排列方法。

  階乘寫法可以參考第  題。

  提示

  求100!展開後的數字