線上教室

繪圖動畫基礎-形狀篇

講義

畫直線(座標軸) Path

早期電腦的繪圖系統或遊戲畫面，都是以「點」(pixel)為基礎，以整數值計算，雖然較節省CPU時間，但圖形放大後會出現鋸齒狀的邊緣，顯得不夠精緻。

Canvas 與 Core Graphics 的繪圖系統則源自 Apple 的 Quartz 2D 框架，是以「向量」(Vector)為設計基礎，能夠在不同設備或不同座標系間轉換，放大縮小完全不失真，計量數值則採用實數。

所謂「向量」(Vector)，是指有方向性的(直線)線段，一條線段有兩個端點，向量會區分起點和終點。因此，在Canvas中的繪圖，是以向量線條為基本要素，可以畫直線、折線、弧線、曲線，再由線條構成各種形狀(Shape)。

在SwiftUI 中畫線條，需要一個 Path 物件，Path 字面意思是「路徑」，但在本課稱之為「畫筆」，較容易理解。以下程式片段，會在圖層中畫出水平中線與垂直中線：

Canvas { 圖層, 尺寸 in
   let 寬 = 尺寸.width
   let 高 = 尺寸.height
   let 中心 = CGPoint(x: 寬/2, y: 高/2)
   let 上中 = CGPoint(x: 寬/2, y: 0)
   let 下中 = CGPoint(x: 寬/2, y: 高)
   let 左中 = CGPoint(x: 0, y: 高/2)
   let 右中 = CGPoint(x: 寬, y: 高/2)
   var 畫筆 = Path()
   畫筆.move(to: 上中)
   畫筆.addLine(to: 下中)
   畫筆.move(to: 左中)
   畫筆.addLine(to: 右中)
   圖層.stroke(畫筆, with: .color(.blue), lineWidth: 1)
}

前7行定義各點位置，後6行分別對應以下6個動作，相對位置請參考下圖：

1. var 畫筆 = Path() 取得一支新的畫筆
2. 將畫筆移(move)到「上中」點
3. 從現在位置「上中」畫直線(addLine)到「下中」為止，畫成垂直中線
4. 提筆移(move)到「左中」點
5. 畫直線(addLine)到「右中」點，完成水平中線，這時候還不會顯示在螢幕上
6. 用圖層的「筆觸」(stroke)並指定顏色與線寬(lineWidth)，才真的顯示在螢幕上

記得，用「畫筆」(Path)猶如在心中描繪，只見影不見人，要等揮毫(stroke)落到「圖層」(context)後，才會現出真形，顯示在螢幕。所以不用每畫一筆，就呼叫一次圖層，而是將整個圖案畫完之後，再用圖層顯示出來。

下表是 Path 物件「畫筆」的物件方法，用來描繪各種線條，本單元會示範前面6個比較重要的功能，後面6個相對容易，可以自行嘗試：

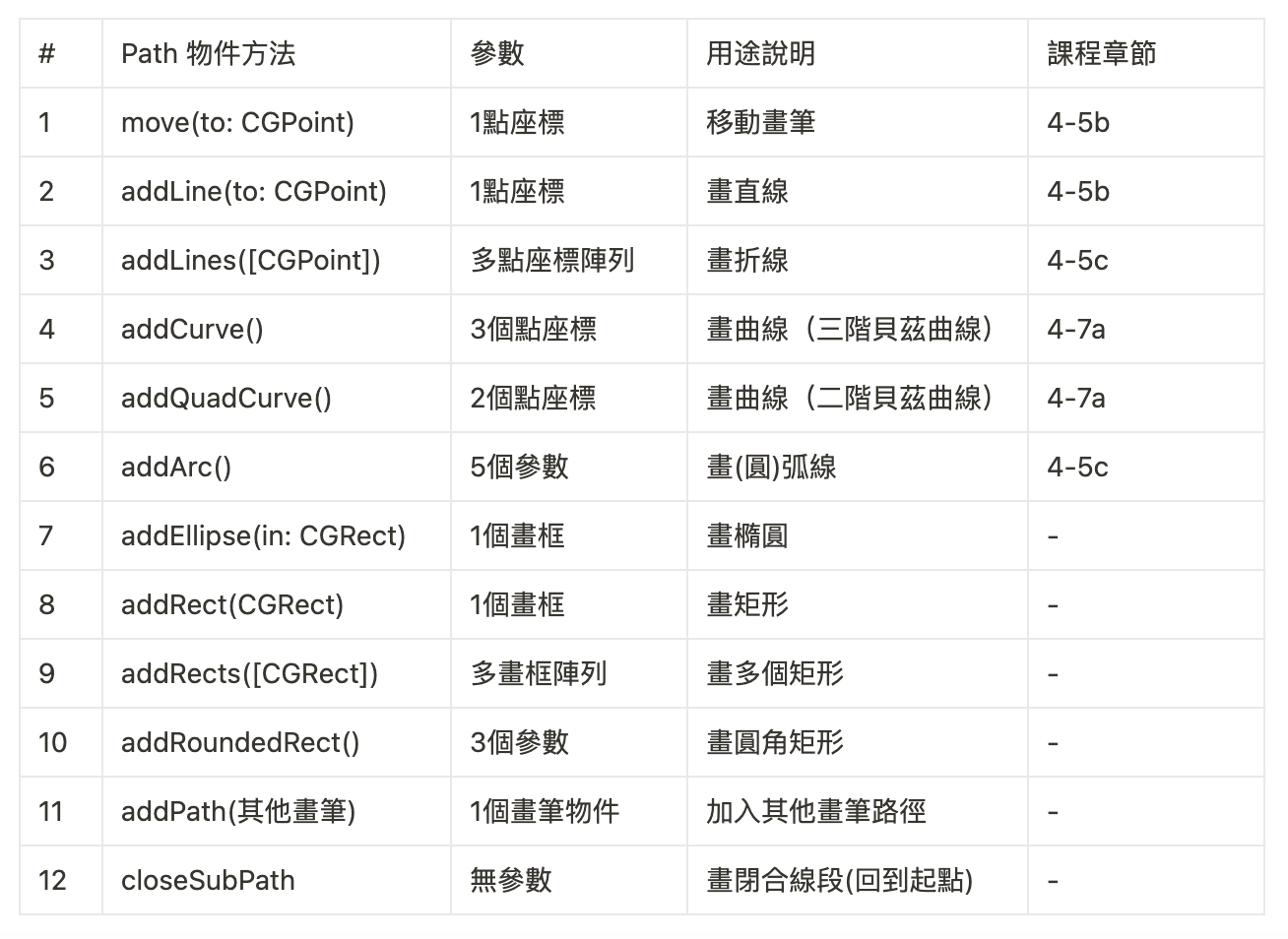
本單元先熟悉 move() 與 addLine() 畫直線的方法。畫完中線後，我們將中線每隔10點加上「刻度」：

var 刻度 = 0.0
while 刻度 < 中心.x {
   let 起 = 中心.y - 3 
   let 訖 = 中心.y + 3
   畫筆.move(to: CGPoint(x: 中心.x - 刻度, y: 起))
   畫筆.addLine(to: CGPoint(x: 中心.x - 刻度, y: 訖))
   畫筆.move(to: CGPoint(x: 中心.x + 刻度, y: 起))
   畫筆.addLine(to: CGPoint(x: 中心.x + 刻度, y: 訖))
   刻度 += 10.0
}

這段程式碼會在水平軸中心兩側各加一條垂直短線，當作水平軸刻度，每10點畫一條刻度：

用同樣方法，再給垂直軸加上刻度。刻度還可以進一步改善，除了每10點一條刻度之外，每50點的刻度可以稍長一些，這樣看起來比較清楚。只要將上面起、訖兩行改成：

let 起 = (刻度.remainder(dividingBy: 50) == 0) ? 中心.y-6 : 中心.y-3 
let 訖 = (刻度.remainder(dividingBy: 50) == 0) ? 中心.y+6 : 中心.y+3

若是整數求餘數，我們可以用 % 符號，至於對實數求餘數，須用物件方法 remainder()，remainder 就是英文「餘數」，參數 dividingBy 則是「除以」。

另外，為了示範多個「圖層」，我們將水平軸與垂直軸分別畫在兩個圖層上，新增圖層的方法很簡單，進入 Canvas { } 之後，用 var 新圖層 = 圖層就可複製空白圖層，最後在畫垂直軸時，以新圖層.stroke() **即可。

操作步驟如下:

選取畫面左方的「+」號新增電子書頁面。

將新增的電子書面頁命名為「(31)SwiftUI動畫-6形狀篇」。

在「Main」模組中撰寫程式:

// 4-5b 直線(座標軸) Path 
// Created by Philip, Heman, Jean 2022/04/19
// Revised by Jean 2025/01/26
import PlaygroundSupport
import SwiftUI

struct 座標軸: View {
   var x = true
   var y = true
   var body: some View {
       Canvas { 圖層, 尺寸 in
           var 新圖層 = 圖層
           let 寬 = 尺寸.width
           let 高 = 尺寸.height
           let 中心 = CGPoint(x: 寬/2, y: 高/2)
           let 上中 = CGPoint(x: 寬/2, y: 0)
           let 下中 = CGPoint(x: 寬/2, y: 高)
           let 左中 = CGPoint(x: 0, y: 高/2)
           let 右中 = CGPoint(x: 寬, y: 高/2)
           if x == true {
               var 畫筆 = Path()
               畫筆.move(to: 左中)
               畫筆.addLine(to: 右中)
               var 刻度 = 0.0
               while 刻度 < 中心.x {
                   let 起 = (刻度.remainder(dividingBy: 50) == 0) ? 中心.y-6 : 中心.y-3 
                   let 訖 = (刻度.remainder(dividingBy: 50) == 0) ? 中心.y+6 : 中心.y+3
                   畫筆.move(to: CGPoint(x: 中心.x+刻度, y: 起))
                   畫筆.addLine(to: CGPoint(x: 中心.x+刻度, y: 訖))
                   畫筆.move(to: CGPoint(x: 中心.x-刻度, y: 起))
                   畫筆.addLine(to: CGPoint(x: 中心.x-刻度, y: 訖))
                   刻度 += 10.0
               }
               圖層.stroke(畫筆, with: .color(.gray), lineWidth: 1)
           }
           if y == true {
               var 畫筆 = Path()
               畫筆.move(to: 上中)
               畫筆.addLine(to: 下中)
               var 刻度 = 0.0
               while 刻度 < 中心.y {
                   let 起 = (刻度.remainder(dividingBy: 50) == 0) ? 中心.x-6 : 中心.x-3 
                   let 訖 = (刻度.remainder(dividingBy: 50) == 0) ? 中心.x+6 : 中心.x+3
                   畫筆.move(to: CGPoint(x: 起, y: 中心.y+刻度))
                   畫筆.addLine(to: CGPoint(x: 訖, y: 中心.y+刻度))
                   畫筆.move(to: CGPoint(x: 起, y: 中心.y-刻度))
                   畫筆.addLine(to: CGPoint(x: 訖, y: 中心.y-刻度))
                   刻度 += 10.0
               }
               新圖層.stroke(畫筆, with: .color(.cyan), lineWidth: 1)
           }
       } 
   }
}

struct 畫布: View {
   @State var showX = true
   @State var showY = true
   var body: some View {
       ZStack(alignment: .bottomTrailing) {
           座標軸(x: showX, y: showY)
           VStack {
               Toggle("X軸", isOn: $showX)
               Toggle("Y軸", isOn: $showY)
           }
           .frame(width: 100)
           .font(.title)
       }
   }
}

// PlaygroundPage.current.setLiveView(座標軸(y: false))
PlaygroundPage.current.setLiveView(畫布())

程式執行結果，如下圖。

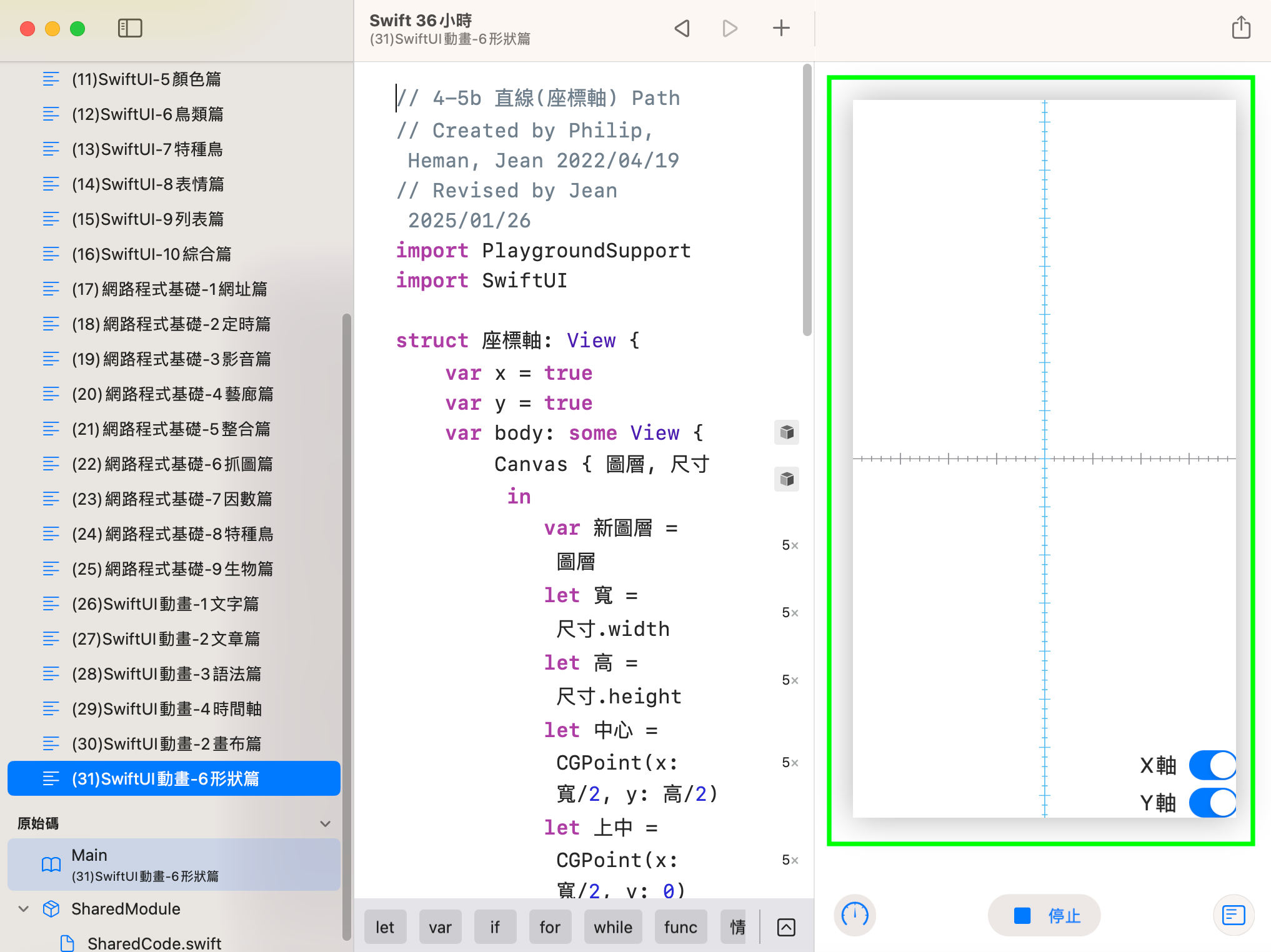
圓與正三角形 Canvas + Path

每個中學生都學過「尺規作圖」，這是從古希臘「幾何原本」流傳下來的作圖方法，到17世紀笛卡兒發明座標系統後，演變成解析幾何，將空間數值化，成為現代科學的重要基礎，不管是用手機GPS定位，還是要登陸火星，都離不開座標與幾何。

解析幾何也是電腦繪圖的數學基礎，圓與三角形是其中最基本的幾何圖形，本節將學習如何在Canvas畫布上，繪製一個圓與內接正三角形。

在「Main」模組中撰寫程式:

// 4-5c 圓與正三角形 Canvas + Path.addArc()
// Created by Philip, Heman, Jean 2022/04/21
// Revised by Jean 2025/01/26
import PlaygroundSupport
import SwiftUI

struct 圓形: View {
   var body: some View {
       Canvas { 圖層, 尺寸 in
           let 寬 = 尺寸.width
           let 高 = 尺寸.height
           let 中心 = CGPoint(x: 寬/2, y: 高/2)
           let 半徑 = min(寬, 高) / 2
           var 畫筆 = Path()
           畫筆.addArc(
               center: 中心,
               radius: 半徑,
               startAngle: .zero,
               endAngle: .degrees(360),
               clockwise: false
           )
           圖層.stroke(畫筆, with: .color(.blue), lineWidth: 2)
       } 
   }
}

struct 正三角形: View {
   var body: some View {
       Canvas { 圖層, 尺寸 in
           let 寬 = 尺寸.width
           let 高 = 尺寸.height
           let 中心 = CGPoint(x: 寬/2, y: 高/2)
           let 半徑 = min(寬, 高) / 2
           let 弧度 = CGFloat.pi * 120 / 180
           let 頂點 = CGPoint(x: 中心.x, y: 中心.y - 半徑)
           let 右 = CGPoint(
               x: 中心.x + 半徑 * sin(弧度), 
               y: 中心.y - 半徑 * cos(弧度))
           let 左 = CGPoint(
               x: 中心.x + 半徑 * sin(弧度*2), 
               y: 中心.y - 半徑 * cos(弧度*2))
           var 畫筆 = Path()
           畫筆.addLines([頂點, 右, 左, 頂點])
           圖層.stroke(畫筆, with: .color(.blue), lineWidth: 2)
       } 
   }
}

struct 畫布: View {
   var body: some View {
       Label("[SwiftUI] 4-5c 圓與正三角形", systemImage: "swift")
           .font(.largeTitle)
           .foregroundColor(.orange)
           .padding()
       ZStack {
           // 座標軸()
           圓形()
           正三角形()
       } .border(Color.gray)
       Text("\(Date())")
           .padding()
   }
}

PlaygroundPage.current.setLiveView(畫布())

程式執行結果，如下圖。

* 說明

在Canvas中畫弧線的方法 addArc() 是畫筆(Path)中較複雜的一個，需要5個參數：

let 半徑 = min(寬, 高) / 2
畫筆.addArc(
   center: 中心,              // 圓心位置座標(CGPoint)
   radius: 半徑,              // 半徑(CGFloat)
   startAngle: .zero,        // 起始角度(Angle)
   endAngle: .degrees(360),  // 終止角度(Angle)
   clockwise: false          // 是否順時針方向(Bool)
)

圓心位置取螢幕中心點，半徑則選寬、高較短者的一半，其中利用全域函式 min() 取參數中的最小值，另一個相對的函式 max() 則是取最大值。

起始角度與終止角度的計算，是以圓心正右方（3點鐘方向）為0°，角度資料類型為 Angle，可用度數或弧度（弳度）來表示，例如 Angle(.degrees(90.0))表示90°，等於弧度𝜋/2，也就是 Angle(.radians(.pi/2))，注意 degrees 和 radians 是用複數名詞。Angle(.zero)表示0°或弧度0，從0°畫到360°就會畫出整個圓。

addArc()最奇特的是最後一個參數，如果設 clockwise: false，實際在螢幕上看到的會是順時針方向，怎麼會這樣？這是因為經過座標轉換，在數學座標中是逆時針方向，到了螢幕座標變成順時針。圖解如下，如果不是畫整個圓，這個參數就會影響畫出的結果：

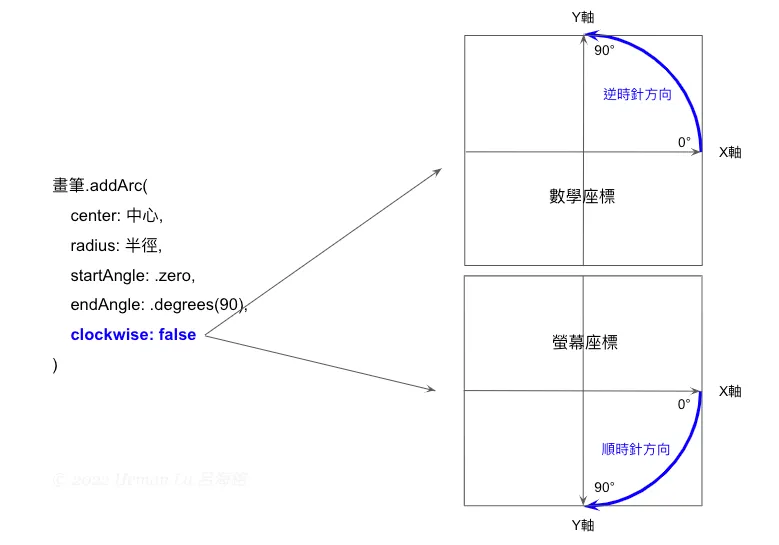
畫出圓形之後，我們要利用圓周來畫正三角形，因為正三角形的3個頂點到圓心的距離等於半徑，並且三等分整個圓，就可利用三角函數來計算3個頂點的座標，三角函數的計算我們到下一課再詳細說明。

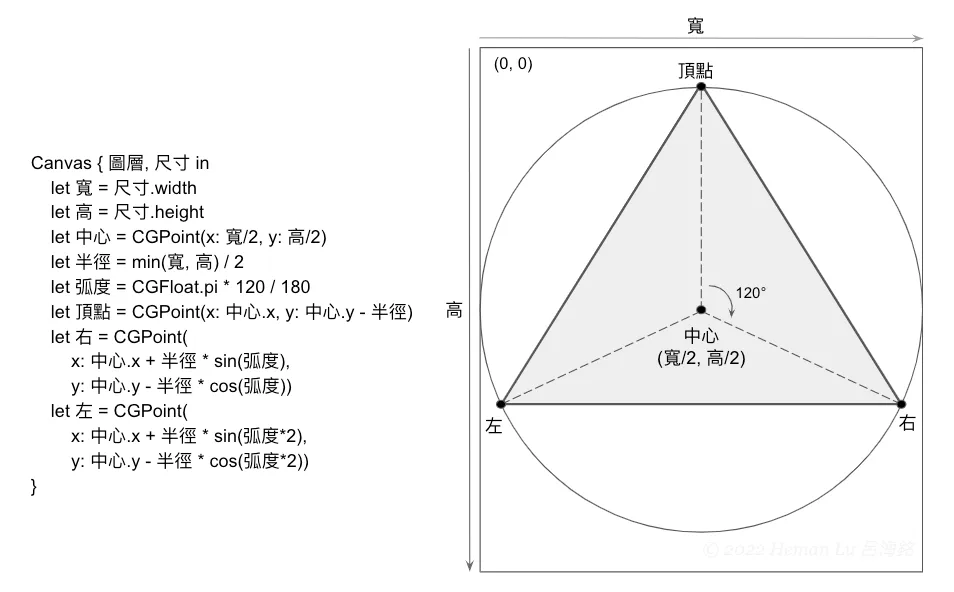
算出三個頂點座標之後，畫三角形就很簡單了，利用 addLines() 可以一口氣畫出多條線段，參數陣列中給4個點，就畫成一個三角形：

var 畫筆 = Path()
畫筆.addLines([頂點, 右, 左, 頂點])
圖層.stroke(畫筆, with: .color(.blue), lineWidth: 2)